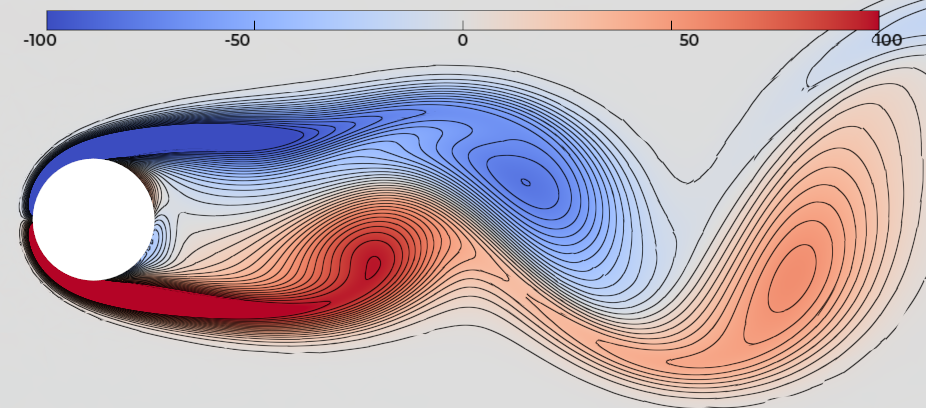
Initialement, mes activités de recherche portaient sur l'analyse de systèmes d'équations aux dérivées partielles (EDP), en particulier dans le domaine de la dynamique des fluides. Dans ce cadre, j'ai notamment décrit le comportement en grand temps des fluides non newtoniens de grades 2 et 3, au travers de leur décomposition en profils asymptotiques. Ces résultats montrent un retour au repos explicite et similaire au cas des fluides newtoniens, régis par les équations de Navier-Stokes. Par la suite, j'ai étudié l'existence et l'unicité de solutions pour une version hyperbolique des équations de Navier-Stokes, pour laquelle la vitesse de propagation de l'information est finie, contrairement aux équations de Navier-Stokes.
Depuis 2015 et le début de mon post-doctorat à l'Inria Saclay dans l'équipe
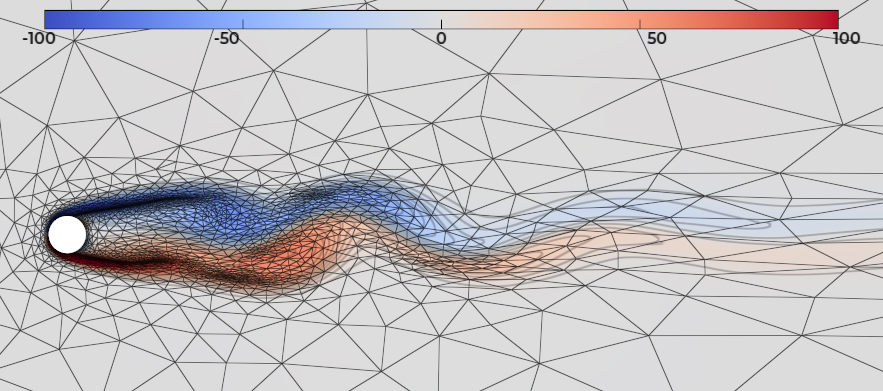
Gamma, ma recherche s'est orientée vers l'adaptation de maillage, en particulier pour les schémas numériques d'ordre élevé. Aujourd'hui, mes développements numériques dans cette thématique sont implémentés dans le logiciel libre
MAdLib, qui est développé et hébergé dans le centre de recherche en aéronautique
Cenaero. Cette librairie permet, à partir d'un maillage initial, de générer un maillage adapté à une solution d'ordre élevé arbitraire, minimisant l'erreur d'interpolation induite par sa projection sur un espace d'éléments finis. Plus récemment, MAdLib a été couplée à la librairie
OpenCascade, permettant de générer des maillages courbes, adaptés à un modèle surfacique donné. Mes activités de recherche au sein de Cenaero m'ont amené à traiter d'autres problématiques liées à la génération d'un maillage satisfaisant pour une application donnée. Par exemple, en partenariat avec
Sonaca, j'ai développé une méthode d'adaptation de maillage permettant de générer des maillages conformes à une ligne de niveau, tout en conservant une qualité de maillage raisonnable. Ci-dessous, vous trouverez quelques exemples d'application de ces méthodes d'adaptation de maillage. Les images ont été produites par le logiciel de visualisation
Vizir, développé par l'Inria.
Adaptation de maillage par rapport à une ligne de niveau, donnée par une optimisation topologique. L'objectif de ce travail est d'optimiser une boîte à rouleau nécessaire au déploiement de becs de bord d'attaque d'une aile d'avion. Le but est de réduire le poids de la pièce, tout en satisfaisant une certaine résistance aux efforts et une faisabilité par fabrication additive. À partir d'un maillage englobant toute la pièce, une surface optimale est calculée par le logiciel Morfeo, sous la forme d'une fonction level-set, c'est à dire une distance signée à la surface optimisée. Une méthode d'adaptation spécifique implémentée dans MAdLib permet alors d'extraire un maillage conforme à l'iso zéro de cette fonction. Le maillage est composé de tétrahèdres linéaires, la surface optimisée est celle de couleur rose.




 t=0.025s
t=0.025s
 t=0.35s
t=0.35s
 t=0.65s
t=0.65s
 t=1.2s
t=1.2s
 t=1.5s
t=1.5s
 t=1.7s
t=1.7s